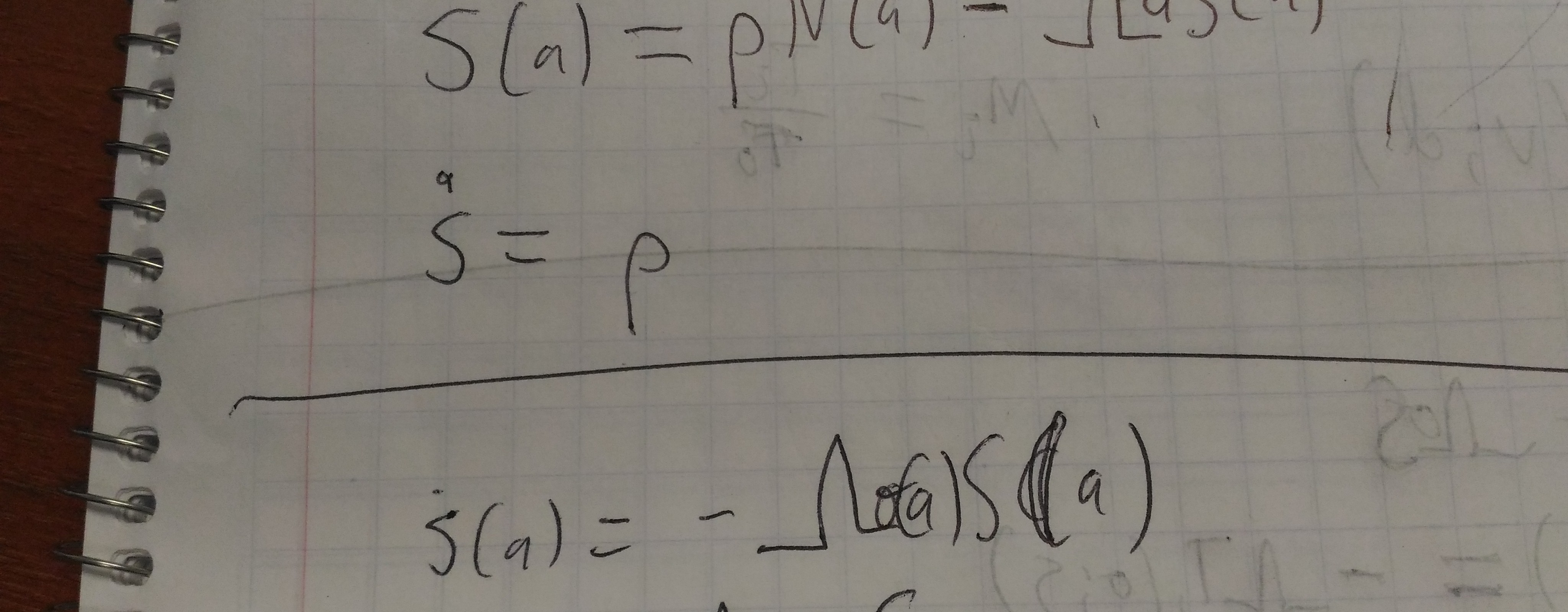Sucker bet
Walt sent me this puzzle (reworded from this set of great puzzles from Communications of the ACM; you can get it by accessing from a University or library).
Alice and Bob roll 2 standard 6-sided dice, note their sum, and repeat. Alice wins if a 7 is rolled, and then followed immediately by another 7. Bob wins if an 8 is followed immediately by a 7. They continue rolling until somebody wins. Who has the better odds of winning?
Of course the answer is the non-intuitive one. Can you figure out why? As a person with a long-time fondness for craps (I know lots of people who are no good at probability, except when it involves two dice), this seems to me like the ultimate sucker bet to offer someone.
Demonstration
The true probability of Alice winning is 47.0%.
This R script simulates 50000 trials and gets 47.0% also.
Answers
I’ve written up some ways to think about the answer, if you’re sure you’re ready to look. Here’s an excerpt that you might want to think about, before clicking:
If we look at all consecutive pairs, the naive probabilities must apply: on average 6 out of every 216 pairs must be 7-7 and 5 out of every 216 must be 8-7. On the other hand, if Alice and Bob play the game forever, Bob will win a majority of times. How is this even possible?