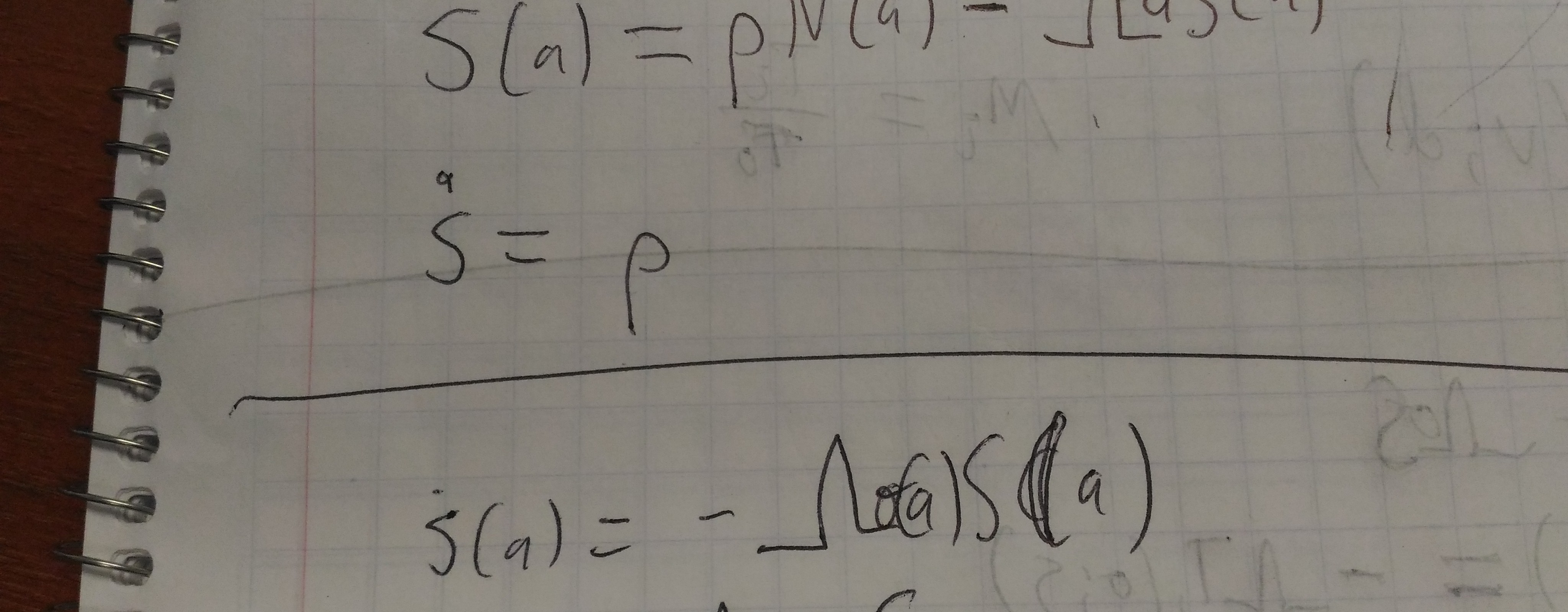Sucker answer

Intuitive argument

We call the numbers each player needs to get to before they win their “point” – Alice’s point is 7, and Bob’s is 8. Each player needs to first get to their point, and then roll a 7 to win.

Common sense tells us we’re more likely to get to Alice’s point than Bob’s, and this is exactly correct. But consider what happens once we get there. If we roll a 7, then Alice wins; if we roll some irrelevant number, we go back to the beginning – it’s the same as if nothing has happened at all; and if we roll an 8, we “jump” to Bob’s point. Similarly, if we are at Bob’s point then either: Bob wins; we go back to the beginning; or we stay at Bob’s point.

It would be great to have a simple diagram here!

Thus, Alice has one advantage (her point is easier to get to), but Bob has two: we can stay at his point, or we can jump there from Alice’s point. As we’ll see, each of these two advantages is a little smaller than Alice’s advantage; together, they are bigger.

Calculation

We call the probability of getting to Alice’s point from the starting position \(p_A = 1/6\), and the probability of getting to Bob’s point \(p_B=5/36\). The relative odds of these two is 6:5, which is the strength of Alice’s initial advantage.

We have another route to Bob’s point, though. Getting there through Alice’s point from the start is 1/6 as likely as going directly. So the total probability of going from start to Bob’s point is 7/6 as likely as going directly. This changes our starting odds by a factor of 6:7

Finally, the probability of winning before leaving Bob’s point (taking into account the probability of staying) is 36/31 times greater than the probability of winning directly. This is because there are 5 ways to stay on the point, and thus 31 total ways to leave, out of a total of 36. So we have another factor of 31:36.

Multiplying (6:5)(6:7)(31:36) gives the correct odds for Alice winning of 31:35.

This may seem fast and loose. Rather than filling in all the details with argument, I’ll try a more direct calculation.

Direct argument

We can write simultaneous equations for the probability of Alice winning \(W_s\) from each of the three possible states of the system, by looking at the probability of going to any other state, or winning, or losing.

Call the states 0 (starting state); A (Alice’s point); and B. The probability of moving from 0 to state \(s\) is called \(p_s\) – these are also the probabilities of where you move from other states, except that sometimes somebody wins instead.

Alice’s winning probability for the game is:

\(W_0 = p_0 W_0 + p_A W_A + p_B w_B\).

If Alice’s point is rolled when we’re already at her point, she just wins, so:

Similarly, if Alice’s point is rolled when we’re at Bob’s point, she just loses:

We solve these simultaneous equations to get:

\(W_0 = \frac{(1-p_B)p_A}{(p_A+p_B)}\), corresponding to odds for Alice of

\(\frac{p_A}{1+p_A} : \frac{p_B}{1-p_B}\).

Substituting \(p_A = 1/6\) and \(p_B = 5/36\) yields the same odds we got in the previous section.

Backward argument

This is my favorite.

If we look at all consecutive pairs, the naive probabilities must apply: on average 6 out of every 216 pairs must be 7-7 and 5 out of every 216 must be 8-7. On the other hand, if Alice and Bob play the game forever, Bob will win a majority of times. How is this even possible?

Well, there must be some 7-7 combinations that don’t end the game. Every game ends with a 7, and one sixth of the time, the next game will start with a 7. This resolves the paradox, and provides a way to calculate the solution:

If the odds of Alice winning are \(A:B\), the total number of 7-7 and 8-7 pairs satisfy \(A + 1/6 A + 1/6 B: B\). This must equal \(6:5\), so we cross multiply (and also multiply both sides by 6):

\(30 A + 5 A + 5 B = 36 B\), or \(35A = 31B\).

Thinking backwards gives the computationally simplest way to get the answer!

And there’s something else cool here. The way that expectations balance out means that, in some real sense, 7-7 is less likely to be achieved first because it’s more likely to be achieved repeatedly.

Please see my blog post on this subject to comment.