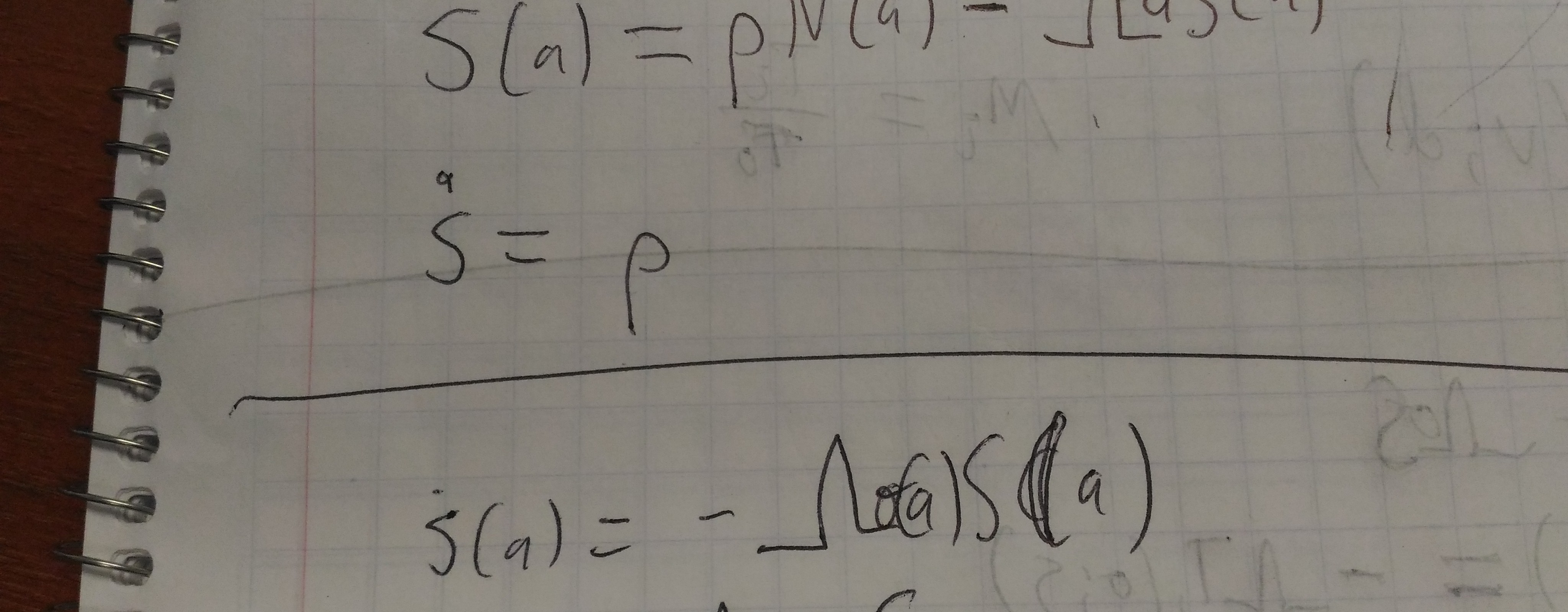Quantile-based distributions
There are various applications where you might want to go from a set of quantiles (and associated probabilities) to an actual approximate distribution.
In particular:
-
to propagate error in a meta-analysis or synthesis when you have confidence intervals from a published paper (example, the rabies burden paper)
-
to systematically evaluate predictions that are expressed in terms of quantiles (see Johansson’s dengue contest stuff, which I cannot find)
There are then two steps:
-
parameterizing a distribution that matches (or approximates) the given quantiles
-
doing something else, either:
- calculating a density to attach likelihood to particular values
- resampling from the distribution
I’ve been trying two different approaches to this:
-
skew normal. There is working code to parametrize and sample, but I suddenly gave up on the density part because I was frustrated that the skew normal couldn’t match things with very high skew. This can match exactly three quantiles (when it can).
-
Johnson-SU distributions. These involve sinh transformations of the normal distribution. This can match four quantiles, which will rarely be wanted, so we need some sort of constraint to restrict the parameter space and get a canonical distribution for three quantiles.
Ben Bolker also has code which works using monotonic splines, which seems less elegant (and therefore possibly less defensible, especially for post hoc application), but definitely more flexible (in particular, can be used for either 3 or 5 parameters).
The method should be:
-
designed to work on an unbounded scale; thus to match probabilities you should first transform to a log odds scale, and to match positive quantities you should first take the log
-
based on the normal distribution (on the transformed scale); in particular, if both the probabilities and quantile values are symmetric on that scale, we should match the normal
-
affine; meaning that if two sets of quantiles differ only by location and scale (on the transformed scale), the method should map them to two distributions which also differ only by location and scale.
Johnson distributions
A deviate \(x\) from a Johnson distribution is obtained by transforming a deviate \(z\) from a normal distribution.
I changed the parameterization somewhat, partly because I want to put the non-trivial scaling step inside the sinh transformation for numerical stability.
I am using:
- \[z = z_0+\mu\]
- \[j_0 = \sinh(s z)/s\]
- \[j = \lambda j_0 + \varepsilon\]
The starting point \(z_0\) is a standard normal, and the ending point \(j\) is the desired Johnson distribution.
\(\lambda\) and \(\varepsilon\) determine the location and scale of the resulting Johnson distribution. We therefore need to use \(\mu\) and \(s\) to determine the shape.
The most appealling idea is to fix \(s=1\). This works well, but limits the amount of skew that can be achieved, so we can’t fit every case. The other idea that seems appealling is to fix \(\mu=0\); in this case, the resulting Johnson distribution is symmetric, which is not at all what we want.
The next simplest constraint, in my opinion, is \(\mu = s\equiv\phi\). This has the advantage of being symmetric and normal when \(\phi=0\). I wrote some code to find to find and calculate densities from these constrained Johnson distributions.
Density calculation
This calculation is boring, especially if it’s right, but I may as well write it down:
-
\(j = λ τ(z; s)\), where τ is the scaled sinh transformation.
-
\(dj = λ τ'(z; s) dz\).
-
\(\frac{f(z)}{ λ τ'(z; s)} dj = f(z) dz\).
-
\(g(j) = \frac{f(z)}{ λ τ'(z; s)}\), where \(g\) is the density over \(j\).
We also have:
- \(τ = \sinh(sx)/s\).
- \(τ' = \cosh(sx)\). Simpler than expected!
This is in fact boring: I have validated that it can be used to produce correct densities when implemented in R.