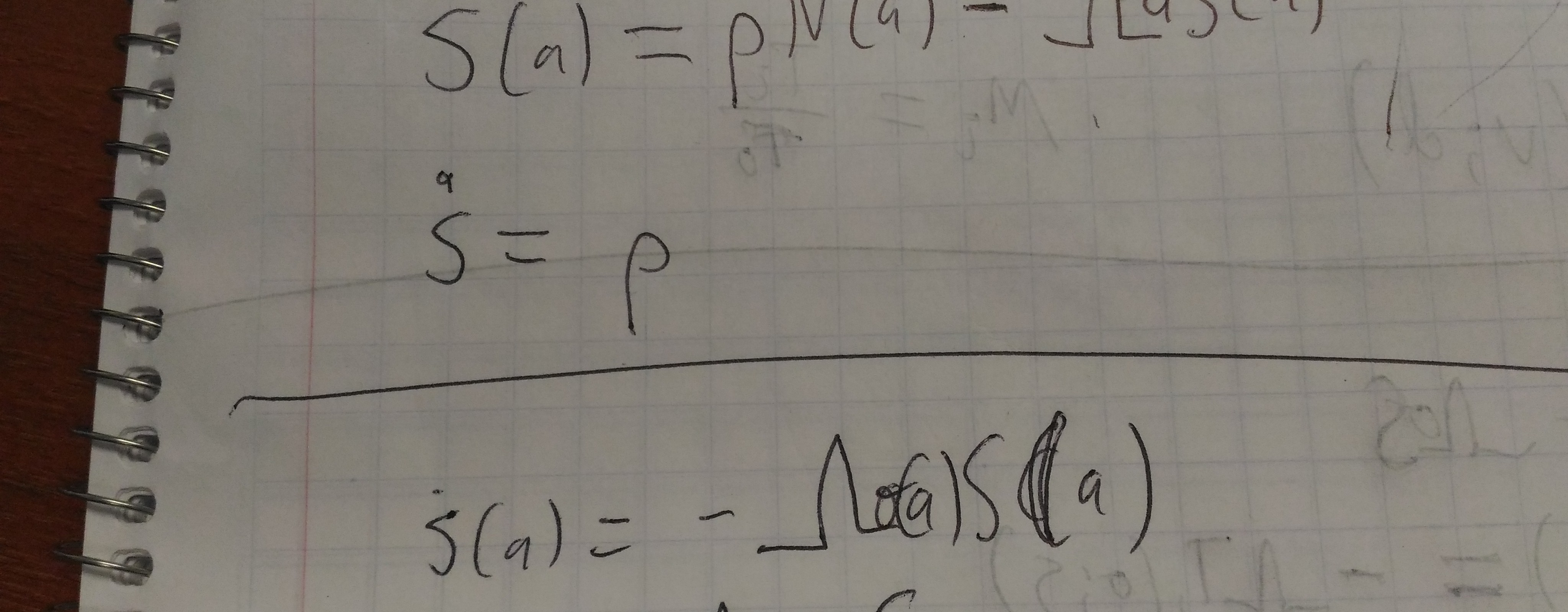Filled circle
Gavin wrote me to say:
Divide a square and a circle each into two complementary subsets that are pairwise similar: S_1;S_2, C_1;C_2, with S_1~C_1, S_2~C_2.
I was confused …
This one seems beyond me. How could it be possible? Is this a weird Hausdorff, axiom-of-choice thing?
If I am interpreting correctly, it means the same as: divide a square into two pieces, and reassemble them into a circle (or conversely). Is that right?
But eventually remembered learning in high school that “similar” and “congruent” are not actually the same thing, and realized that I could just do this:

or even this: