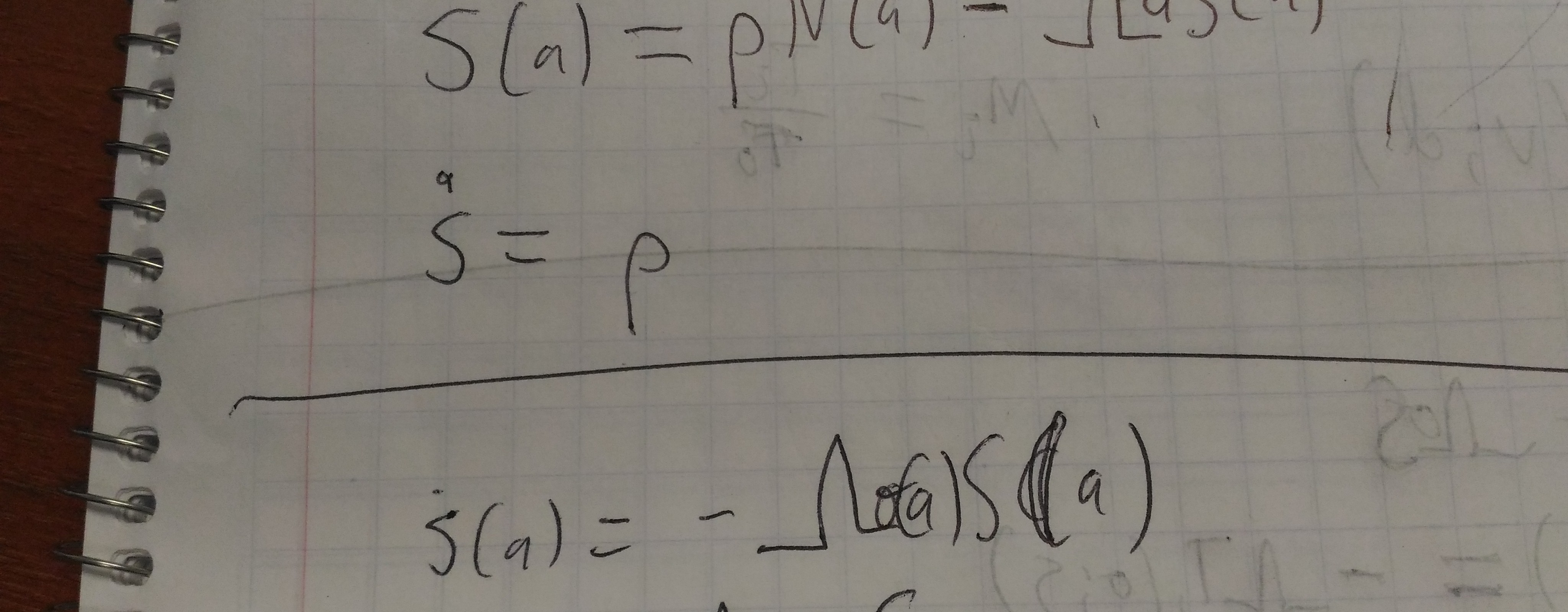The standard equation for fitting a growing epidemic is \(\dot x = \lambda x\), yielding

\[x(t) = x_0 \exp(\lambda t).\]

The next simplest thing (or at least, one alternative for the next simplest thing), is \(\dot x = \lambda x^{1-b}\), yielding

\[x(t) = (x_0^b + \lambda t b)^{1/b}.\]

These match if we take the limit as \(b\to 0\). If \(b>0\), we get sub-exponential growth, whereas \(b<0\) leads to super-exponential growth, with divergence at the finite time \(t_d = \frac{-x_0^b}{b\lambda}\).

Note that this formulation is usually used for prevalence, but I guess it would work to fit it to incidence as well. It would be interesting to compare to the Chowell et al. cumulative-incidence based framework.

Fitting details

To fit, we want to constrain \(x_0>0\), \(\lambda>0\) and \(b>b_c\), where \(b_c\) is the root of a difficult equation. We could avoid the difficult equation if we let \(b\) be unconstrained, and instead constrain \(x_0\) on both ends (so that it’s not big enough to diverge). Having \(x_0\) be sometimes one-sided and sometimes two-sided seems awkward, though.