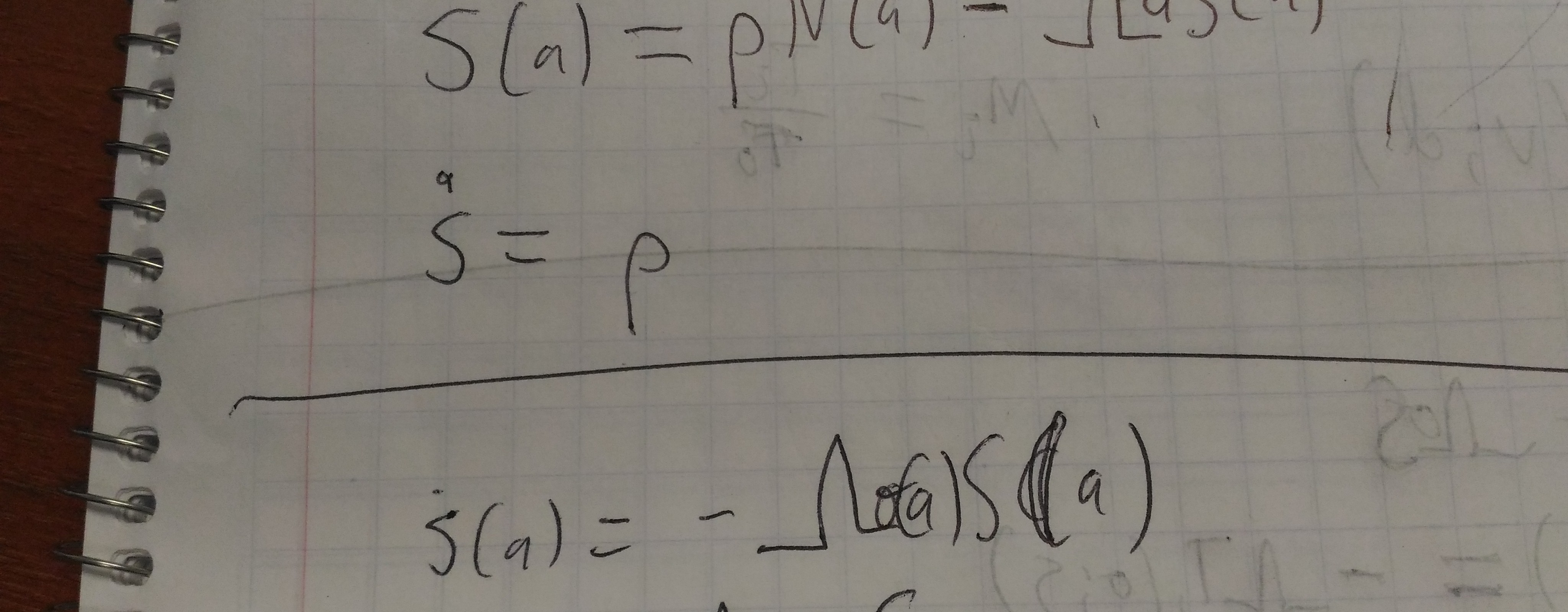Conditional kernels
Framework
We imagine kernels indexed across an aspect space $A$. Thus the unconditional, population-level kernel is:
\[k(\tau) = \int{k_a(\tau) dA}\]The conditional kernel for an individual is:
\[\hat k(\tau) = k_a(\tau)\exp\left(-\delta_a \int_0^\tau{k_a(\sigma) d\sigma}\right)\]\(\delta\) is the dilution (one over something-about-degree). Dilution could be individual-specific or not.
The conditional kernel for the population is:
\[\hat k(\tau) = \int{\hat k(\tau) dA}\]SIR
SIR corresponds to \(k_D(\tau) = \beta H(D-\tau)\); \(dA = \gamma\exp\left(-\gamma D\right)\,dD\), where \(D\) is the duration of an individual infection.
The kernel is thus:
\[k(\tau) = \int{\beta H(D-\tau) \gamma\exp\left(-\gamma D\right)\,dD}\]where H is the Heaviside function.
We restrict the domain to eliminate H:
\[k(\tau) = \int_\tau^\infty{\beta \gamma\exp\left(-\gamma D\right)\,dD}\] \[= \beta\exp\left(-\gamma\tau\right)\]And the conditional kernel is:
\[\hat k(\tau) = \int{ \beta H(D-\tau) \exp\left(-\delta_a \int_0^\tau{\beta H(D-\sigma) d\sigma}\right) \gamma\exp\left(-\gamma D\right)\,dD }\]\(\sigma\le\tau\) in the inner integral, so when we collapse the outer Heaviside, the inner one just disappears:
\[\hat k(\tau) = \int_\tau^\infty{ \beta \exp\left(-\delta_a \int_0^\tau{\beta d\sigma}\right) \gamma\exp\left(-\gamma D\right)\,dD }\] \[= \beta \exp\left(-\delta_a \beta \tau\right) \exp\left(-\gamma \tau\right)\]